Лекция 3. Описательная статистика. Показатели разброса или вариации

Вариация - это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие   показатели вариации: размах вариации, среднее линейное отклонение, линейный коэффициент вариации, дисперсия, среднее квадратическое отклонение, квадратический коэффициент вариации.

Размах вариации

Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:

H=X_max-X_min

Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.

Cреднее линейное отклонение

Cреднее линейное отклонение   - это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой - получим среднее линейное отклонение простое:

Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5.Ранее уже была рассчитана средняя арифметическая= 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.

Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной - получим среднее линейное отклонение взвешенное:

Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.

Функция СРОТКЛ

  Эта функция вычисляет среднее абсолютных значений отклонений точек данных от среднего, т.е. является мерой разброса множества данных.

Общий вид функции

СРОТКЛ (число1; число2; ...)

Число1, число2, ... - это от 1 до 30 аргументов, для которых определяется среднее абсолютных отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой. При использовании функции надо учитывать следующие условия:

·       аргументы должны быть числами или именами, массивами или ссылками, содержащими числа;

·       если аргумент содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.

Уравнение для среднего отклонения следующее:

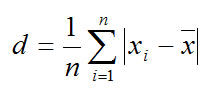
На результат СРОТКЛ влияют единицы измерения входных данных.

Линейный коэффициент вариации

Линейный коэффициент вариации   - это отношение среднего линейного отклонения к средней арифметической:

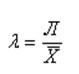
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.

В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.

Дисперсия

Дисперсия - это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой - получим дисперсию простую:

В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4)²+(4-4)²+(4-4)²+(5-4)²)/4 = 0,5.

Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной - получим дисперсию взвешенную:

В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную:
Д = ((3-4)²*1+(4-4)²*2+(5-4)²*1)/4 = 0,5.

Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:

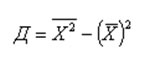
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3²*1+4²*2+5²*1)/4-4²   = 16,5-16 = 0,5.

Если значения X - это доли совокупности, то для расчета дисперсии используют частную формулу дисперсии доли :

.

Функция ДИСПР

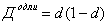Функция вычисляет дисперсию для генеральной совокупности. (Для дисперсии по выборке используется функция ДИСП). Дисперсией (s²) называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней арифметической.

ДИСПР(число1;число2; ...)

Число1, число2, ... - это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Логические значения, например ИСТИНА и ЛОЖЬ, а также текст игнорируются

ДИСПР предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять, используя функцию ДИСП.

Уравнение для дисперсии имеет следующий вид:

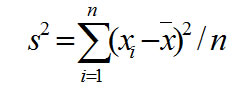
Для функции ДИСП используется формула

Функция ДИСПРА

Функция аналогично ДИСПРА вычисляет дисперсию для генеральной совокупности. В расчете помимо численных значений учитываются также текстовые и логические значения, такие как ИСТИНА или ЛОЖЬ.

ДИСПРА(значение1,значение2,...)

Значение1,значение2,... - это от 1 до 30 числовых аргументов, соответствую щих генеральной совокупности.

ДИСПРА предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять, используя функцию ДИСПА. Аргументы, содержащие значение ИСТИНА интерпретируются как 1, аргументы, содержащие текст или значение ЛОЖЬ интерпретируются как 0 (ноль).

Cреднее квадратическое отклонение

Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:

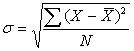
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:

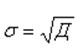
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее: .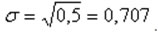

Функция КВАДРОТКЛ

При определении вариации часто используется функция, которая возвращает сумму квадратов отклонений точек данных от их среднего.

Общий вид функции

КВАДРОТКЛ(число1;число2;...)

Число1, число2, ... - это от 1 до 30 аргументов, для которых вычисляется сумма квадратов отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. Если аргумент содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.

Уравнение для суммы квадратов отклонений имеет следующий вид:

Функция СТАНДОТКЛОНП

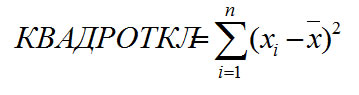
Вместо дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используется среднее квадратическое или стандартное отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значение признака. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.

СТАНДОТКЛОНП(число1; число2; ...)

Число1, число2, ...   - это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой. Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются.

СТАНДОТКЛОНП предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОН. Для больших выборок СТАНДОТКЛОН и СТАНДОТКЛОНП возвращают примерно равные значения.

СТАНДОТКЛОНП использует следующую формулу:

,

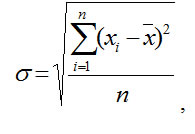а СТАНДОТКЛОН -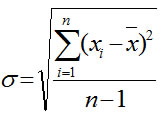

Функция СТАНДОТКЛОНПА

Функция аналогично функции СТАНДОТКЛОНП вычисляет стандартное отклонение по генеральной совокупности. В данном случае аргументами могут являться текст и логические значения.

СТАНДОТКЛОНПА(значение1,значение2,...)

Значение1,значение2,...   это от 1 до 30 значений, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

СТАНДОТКЛОНПА предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОНА. Аргументы, содержащие значение ИСТИНА интерпретируются как 1, аргументы, содержащие значение ЛОЖЬ интерпретируются как 0 (ноль). Для больших выборок СТАНДОТКЛОНА и СТАНДОТКЛОНПА возвращают примерно равные значения.

Квадратический коэффициент вариации

Квадратический коэффициент вариации - это самый популярный относительный показатель вариации:

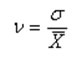
Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 - вариация считает слабой, а если больше 0,333 - сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина -   нетипичной   и ее нельзя использовать как обобщающий показатель этой совокупности.

В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.

Средние величины, характеризуя ряд наблюдений, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Обычно рассматриваются меры наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.

Сумма отклонений результатов наблюдений от средней арифметической не может характеризовать вариацию наблюдений около средней арифметической, т.к. эта сумма равна нулю. Обычно берут или абсолютные величины или квадраты разностей. В результате получают различные показатели вариации: среднее отклонение, дисперсию или среднеквадратичное отклонение.

<<предыдущая || оглавление || следующая>>